3 The cornerstones of statistics
This chapter is an attempt to introduce modern classical statistics. “Modern classical” may sound like a contradiction, but it is in fact anything but. Classical statistics covers topics like estimation, quantification of uncertainty, and hypothesis testing – all of which are at the heart of data analysis. Since the advent of modern computers, much has happened in this field that has yet to make it to the standard textbooks of introductory courses in statistics. This chapter attempts to bridge part of that gap by dealing with those classical topics, but with a modern approach that uses more recent advances in statistical theory and computational methods.
Whenever it is feasible, the aim of this books is to:
- Use hypothesis tests that are based on permutations or the bootstrap rather than tests based on strict assumptions about the distribution of the data or asymptotic distributions,
- Complement estimates and hypothesis tests with confidence intervals based on sound methods (including the bootstrap), and
- Offer easy-to-use Bayesian methods as an alternative to frequentist tools.
After reading this chapter, you will be able to use R to:
- Create contingency tables,
- Run hypothesis tests including the t-test and the \(\chi^2\)-test,
- Compute confidence intervals,
- Handle multiple testing,
- Run Bayesian tests, and
- Report statistical results.
3.1 The three cultures
There are three main schools in statistical modelling: the frequentist school, the Bayesian school, and the machine learning school.
The main difference between the frequentist and Bayesian schools is the way in which they approach probability. Frequentist statistics uses the frequency, or long-run proportion, of an event to describe the probability that it occurs. Bayesian statistics incorporates prior knowledge and personal beliefs about the event to compute subjective probabilities.
Many of the best known tools in the statistical toolbox, such as p-values and confidence intervals, stem from frequentist statistics. It has often been considered a more objective approach, suited for analysing experiments. Bayesian statistics has been considered to be more flexible and adaptable, as it allows for the incorporation of prior knowledge and beliefs and can be updated as new evidence becomes available. This makes it well suited for situations where there is a need to incorporate subjective information or to update predictions as new data becomes available.
Both frequentist and Bayesian statistics have a tradition of theoretical statistics and the development of rigorous, formal mathematical methods for analysing and interpreting data, that can be shown to be optimal in certain scenarios. In contrast, the machine learning school is characterised by a focus on developing algorithms and computational tools for automatically identifying patterns in data and making predictions based on those patterns. This culture is associated with more practical, data-driven approaches to solving problems, and much less rigour. Methods are evaluated by checking whether they give good predictions for test datasets, rather than by their theoretical properties. In recent years, a part of this school has been rebranded as artificial intelligence, or AI.
All three schools are essential parts of modern statistics, and there is a lot of interaction between them (for instance, methods from frequentist and Bayesian statistics are often used in machine learning). In this book, we’ll make use of tools from all three schools. For statistical analyses in this chapter and in Chapters 7-10, we’ll focus on frequentist methods but offer Bayesian methods as a useful alternative and describe their advantages. Chapter 11 is devoted to the machine learning mindset and its use in predictive modelling.
3.2 Frequencies, proportions, and cross-tables
Some statistical tools are equally important in all three statistical schools. Among them are frequency tables and contingency tables,. We’ll look at some examples using the penguins dataset from the palmerpenguins package. Let’s start by reading a little about the data:
3.2.1 Frequency tables
Frequency tables are used to summarise the distribution of a single variable. They consist of a list of the different values that a variable can take, along with either the number of times (the frequency) each value occurs in the data, or the proportion of times it occurs. For example, a frequency table for the variable species might show the number of individuals from different species in a dataset, as in this example with the penguins data:
This results in the following output in the Console:
##
## Adelie Chinstrap Gentoo
## 152 68 1243.2.2 Publication-ready tables
The table in the previous section is fine for data exploration but requires some formatting if you wish to put it in a report. If instead you want something publication-ready that you can put straight into a report or a presentation, I recommend using either the gtsummary package or the ivo.table package. Let’s install them (along with the flextable package, which we’ll also need), and see how they can be used to create a frequency table for species using the penguins data:
Let’s start with an example using gtsummary and its tbl_summary function:
We now get a better-looking table. It is shown in the Viewer pane in RStudio. You can highlight it with your mouse cursor to copy and paste it into, e.g., Word or PowerPoint, or use functions from the flextable package to export it to various file formats. Here is an example of how we can export it as a Word document:
library(flextable)
penguins |>
select(species) |>
tbl_summary() |>
as_flex_table() |> # Convert the table to a format that can be exported
save_as_docx(path = "my_table.docx")The ivo.table package and the ivo_table function offer a similar table constructed in the same way:
You can modify the settings to change the colours and fonts used, and to show percentages instead of counts:
If you prefer, you can also get the table in a long format that is useful when your variable has many different levels:
Finally, the table can be exported to Word as follows:
3.2.3 Contingency tables
Contingency tables, also known as cross-tabulations or cross-tables, are used to summarise the relationship between two or more variables. They consist of a table with rows and columns that represent the different values of the variables, and the entries in the table show the number or proportion of times each combination of values occurs in the data. For example, a contingency table for the variables species and island in the penguins data shows the number of individuals of different species at different islands.
The resulting table is:
## Adelie Chinstrap Gentoo
##
## Biscoe 44 0 124
## Dream 56 68 0
## Torgersen 52 0 0Again, we can create a nicely formatted publication-ready table. With ivo_table, we follow the same logic as before:
The settings and export options that we used before are still available:
# Change colours and fonts and export to a Word file named "penguins.docx":
library(flextable)
penguins |> select(species, island) |>
ivo_table(color = "darkred",
font = "Garamond",
percent_by = "tot") |>
save_as_docx(path = "penguins.docx")We can also highlight cells of particular interest. For instance, the cell in the second column (the column with island names counts as a column here) of the third row:
To create a contingency table using tbl_summary, we use the following syntax:
For tables like the ones we just created, it is common to talk about \(R\times C\) contingency tables, where \(R\) denotes the number of rows and \(C\) denotes the number of columns (not including any rows or columns displaying the margin sums). The table in the penguins example above is thus a \(3\times 3\) contingency table.
Contingency tables are great for presenting data, and in many cases we can draw conclusions directly from looking at such a table. For instance, in the example above, it is clear that Adelie penguins are the only species present at all three islands (or at least, the only species sampled at all three islands). In other cases, the results aren’t as clear-cut. That’s when statistical hypothesis testing becomes useful – a powerful set of tools that lets us determine for instance whether there is statistical evidence for differences between groups. We’ll get to that soon, but first we’ll look at some examples of tables for three and four variables.
3.2.4 Three-way and four-way tables
Three-way and four-way tables are contingency tables showing the distribution of three and four variables, respectively. They are straightforward to create using ftable or ivo_table. We simply select the variables we wish to include in the table, and use ftable or ivo_table as in previous examples. Here are some examples using ivo_table:
# A three-way table:
library(ivo.table)
penguins |> select(sex, species, island) |>
ivo_table()
# Exclude missing values:
penguins |> select(sex, species, island) |>
ivo_table(exclude_missing = TRUE)
# A four-way table:
penguins |> select(sex, species, island, year) |>
ivo_table()You can’t use gtsummary to construct three-way and four-way tables, but you can use it for a similar type of table, presenting several variables at once, stratified by another variable. For instance, we can show the frequencies of islands and sexes stratified by species, as in the example below. This type of table, showing the distributions of different categorical variables, is often referred to as Table 1 in scientific papers.
3.3 Hypothesis testing and p-values
Statistical hypothesis testing is used to determine which of two complementary hypotheses that is true. In statistics, a hypothesis is a statement about a parameter in a population, such as the population mean value. The two hypotheses in a hypothesis testing problem are:
- The null hypothesis \(H_0\): corresponding to “no effect”, “no difference”, or “no relationship”.
- The alternative hypothesis \(H_1\): corresponding to “there is an effect”, “there is a difference”, or “there is a relationship”.
To make this more concrete, let’s look at some examples.
The effect of a treatment. To study how a new drug affects systolic blood pressure, we measure the blood pressure of a number of patients twice: before and after they take the drug. The population parameter that we’re interested in is \(\Delta\), the average change in blood pressure between the two measurements. The hypotheses are as follows:
- \(H_0\): there is no effect; \(\Delta=0\).
- \(H_1\): there is an effect; \(\Delta \neq 0\).
Comparing two groups. To find out whether flipper length differs between male and female Chinstrap penguins, we measure the flipper lengths of a number of penguins. If the average length in the female population is \(\mu_1\) and the average length in the male population is \(\mu_2\), then the population parameter that we are interested in is the difference \(\mu_1-\mu_2\). The hypotheses are:
- \(H_0\): there is no difference; \(\mu_1-\mu_2=0\).
- \(H_1\): there is a difference; \(\mu_1-\mu_2 \neq 0\).
The relationship between two variables \(X\) and \(Y\). We are interested in finding out whether the sex distribution for Adelie penguins is the same on three different islands. For a randomly selected Adelie penguin, let \(P(X=x)\) denote the probability that the sex \(X\) takes the value \(x\) (possible values being male and female), and \(P(Y=y)\) that the island \(Y\) takes the value \(y\) (with three different possible values). The hypotheses are:
- \(H_0\): the variables are independent; \(P(X=x \mbox{ and } Y=y)=P(X=x)P(Y=y)\) for all \(x,y\).
- \(H_1\): the variables are dependent; there is at least one pair \(x,y\) such that \(P(X=x \mbox{ and } Y=y)\neq P(X=x)P(Y=y)\).
The purpose of hypothesis testing is to determine which of the two hypotheses to believe in. Hypothesis testing is often compared to legal trials: the null hypothesis is considered to be “innocent until proven guilty”, meaning that we won’t reject it unless there is compelling evidence against it. We can therefore think of the null hypothesis as a sort of default – we’ll believe in it until we have enough evidence to say with some confidence that it in fact isn’t true.
In frequentist statistics, the strength of the evidence against the null hypothesis is measured using a p-value. It is computed using a test statistic, a summary statistic computed from the data, designed to measure how much the observations deviate from what can be expected under the null hypothesis. Bayesian approaches to hypothesis testing are fundamentally different, and are covered in Section 3.9.
The p-value quantifies the amount of evidence as the probability under \(H_0\) of obtaining an outcome that points in the direction of \(H_1\) at least much as the observed outcome. The lower the p-value is, the greater the evidence against \(H_0\). Being a probability, it ranges from 0 to 1.
How this probability is computed depends on the hypotheses themselves, how we wish to measure how much an outcome deviates from \(H_0\), and what assumptions we are prepared to make about our data. Throughout this chapter, we’ll see several examples of how p-values are computed in different situations. We’ll start with an example that inspired the invention of p-values in the 1920s.
3.3.1 The lady tasting tea
The quintessential example of a statistical hypothesis test is that of the lady tasting tea, described by Sir Ronald Fisher in the second chapter of his classic 1935 text The Design of Experiments. A colleague of Fisher’s, the phycologist Dr. Muriel Bristol, took her tea with milk and claimed that she could tell whether milk or tea was added to the cup first. Fisher did not believe her and devised an experiment to test her claim. It consisted of preparing eight cups of tea out of sight of the lady, four in which the milk was poured first, and four in which the tea was poured first. She would then be presented with the cups in a randomised order, tasked with dividing the cups into two groups of four according to how they were prepared.
The hypotheses that this experiment was designed to test are:
- \(H_0\): the lady’s guesses are no better than chance.
- \(H_1\): the lady’s guesses are better than chance.
This is a test of independence – if the lady’s guesses are no better than chance, then her guess (\(X\)) is independent from the content in the cup (\(Y\)).
The results of the experiment can be presented in a \(2\times 2\) contingency table. For instance, one possible outcome is that the lady gets both sets of four right, which yields the following table:
| Truth: milk first | Truth: tea first | |
|---|---|---|
| Guess: milk first | 4 | 0 |
| Guess: tea first | 0 | 4 |
The design of this experiment is such that all row sums and column sums are 4. Consequently, if we know the count in the upper left cell (the number of cups where the milk was poured first correctly identified as such by the lady), we also know the counts in the other cells20. This means that there are 5 possible tables that can result (the count in the upper left cell can be 4, 3, 2, 1, or 0). We can compute the probability of obtaining each table under the null hypothesis21, with the following results:
- The count is 4 (4 cups with milk poured first right), with probability 1/70,
- The count is 3 (3 cups with milk poured first right and 1 wrong), with probability 16/70,
- The count is 2 (2 cups with milk poured first right and 2 wrong), with probability 36/70,
- The count is 1 (1 cup with milk poured first right and 3 wrong), with probability 16/70,
- The count is 0 (4 cups with milk poured first wrong), with probability 1/70.
A high number of correct guesses would be expected if \(H_1\) were true, but not if \(H_0\) were true. Consequently, high counts can be considered to be evidence against \(H_0\). With this in mind, now that we know what the possible outcomes of the experiment are, and how likely they are if \(H_0\) is true, we can compute the p-values corresponding to the different outcomes.
Getting all 4 cups where the milk poured first right is the most extreme outcome, in the sense that among all possible outcomes, this points the most in the direction of \(H_1\), i.e., that the lady’s guesses are better than change. If \(H_0\) is true, this occurs in 1 experiment out of 70. The p-value is therefore \(1/70\approx 0.014\).
Getting 3 cups where the milk poured first right is the second most extreme outcome. If \(H_0\) is true, this occurs in 16 experiments out of 70. In addition, a more extreme outcome (4 cups right) occurs in 1 experiment out of 70. The probability of getting a result that is at least as extreme as this is therefore \(\frac{16}{70}+\frac{1}{70}=\frac{17}{70}\), and the p-value given this outcome is \(17/70\approx 0.24\).
Similarly, we find that if the lady gets 2 cups right, the p-value is \(\frac{36}{70}+\frac{16}{70}+\frac{1}{70}\approx 0.75\), if she gets 1 cup right the p-value is \(0.99\) and if she gets 0 cups right the p-value is \(1\).
At this point, you may be asking why we include outcomes that we in fact haven’t observed when computing p-values. Why don’t we simply compute how unlikely the observed outcome is if \(H_0\) is true? To see why, recall that a low p-value means that we have evidence against \(H_0\), and note that getting 0 cups right is the outcome that is the furthest from what we should expect under \(H_1\). If we used the null probability of this outcome as the p-value, the p-value would become \(1/70\), i.e., rather low, even though we have absolutely no evidence at all that \(H_0\) is false in this case. Including more extreme outcomes in the computation allows us to quantify how extreme the observed outcome is.
3.3.2 How low does the p-value have to be?
We’ve now seen how p-values can be computed in the lady tasting tea example, but we still haven’t seen how to use p-values to make a decision about what hypothesis to believe in. The lower the p-value, the greater the evidence against \(H_0\). But how low does the p-value have to be for us to say that we have sufficient evidence to reject \(H_0\)?
We need some way of determining a cut-off for p-values. Let’s call this cut-off \(\alpha\), the significance level of our test. It can be any number between 0 and 1. Once we’ve decided on a value for \(\alpha\), we are ready to make a decision regarding which hypothesis to believe in. If the p-value is less than \(\alpha\), we reject \(H_0\) in favour of \(H_1\) and say the result is statistically significant. If the p-value is greater than \(\alpha\), we conclude that there isn’t sufficient evidence against \(H_0\), so we’ll believe in it for the time being.
How then shall we choose \(\alpha\)? There are two types of errors that we can make in hypothesis testing:
- A type I error: falsely rejecting \(H_0\) even though \(H_0\) is true (a false positive result).
- A type II error: not rejecting \(H_0\) even though \(H_1\) is true (a false negative result).
Both of these will depend on what significance level we choose for our p-value. If we choose a low \(\alpha\), we require more evidence before we reject \(H_0\). This lowers the risk of a type I error but increases the risk of a type II error. Conversely, if we choose a higher cut-off, we get a higher risk of a type I error, but a lower risk of a type II error.
The probability of making a type I error is the easiest to control and often also considered to be the most important of the two. If we reject \(H_0\) whenever the p-value is less than \(\alpha\), then the probability of committing a type I error if \(H_0\) is true is also \(\alpha\). For this reason, \(\alpha\) is often called the type I error rate. A common choice is to use \(\alpha=0.05\) as the cut-off, meaning that the null hypothesis is falsely rejected \(5 \%\) of all studies where it in fact was true, or that 1 study in 20 finds statistical evidence for alternative hypotheses that are false.
No, wait, let me stop myself right there, because I just lied to you and we probably shouldn’t let that slide. I just claimed that if we reject \(H_0\) when the p-value is less than \(\alpha\), the probability of committing a type I error is also \(\alpha\). Indeed, you’ll see similar statements in many different texts. This is an oversimplification that only is true in idealised situations that no one has ever encountered outside of a classroom. In the real world, there are two types of tests:
- Exact tests, for which the probability of committing a type I error is less than or equal to \(\alpha\).
- Approximate tests, for which the probability of committing a type I error is approximately equal to \(\alpha\) (but may be greater than \(\alpha\), perhaps substantially so). How close it is to \(\alpha\) depends on a number of factors; we’ll discuss these for different tests later in this chapter.
The test that we constructed in the lady tasting tea example is an exact test (which can be seen through deeper mathematical analysis of its properties). It is known as Fisher’s exact test. In the next section, we’ll have a look at how we can use it to analyse data in R.
3.3.3 Fisher’s exact test
To use Fisher’s exact test, we first need some data. The contingency table describing the outcome of the experiment can be constructed in different ways in R, depending on whether our data is stored in a long data frame or already available in tabulated form. If it is stored in a data frame, where each row shows the outcome of a repetition, we can get a contingency table as follows:
# Compute the contingency table from a data frame:
lady_data <- data.frame(Guess = c("Milk first", "Milk first",
"Tea first", "Tea first",
"Milk first", "Tea first",
"Tea first", "Milk first"),
Truth = c("Milk first", "Milk first",
"Tea first", "Tea first",
"Milk first", "Tea first",
"Tea first", "Milk first"))
lady_data |> ftable() -> lady_results1
lady_results1If instead the data already is stored as counts, we can create a contingency table by hand by creating a matrix containing the counts:
# Input the contingency table directly, if we only have the counts:
lady_results2 <- matrix(c(4, 0, 0, 4),
ncol = 2, nrow = 2,
byrow = TRUE,
dimnames = list(c("Guess: milk first", "Guess: tea first"),
c("Truth: milk first", "Truth: tea first")))
lady_results2To perform Fisher’s exact test, for the lady tasting tea data, we use fisher.test as follows:
fisher.test(lady_results1, alternative = "greater")
fisher.test(lady_results2, alternative = "greater")The output contains the p-value (\(0.01429\)), and some additional information:
##
## Fisher's Exact Test for Count Data
##
## data: lady_results2
## p-value = 0.01429
## alternative hypothesis: true odds ratio is greater than 1
## 95 percent confidence interval:
## 2.003768 Inf
## sample estimates:
## odds ratio
## Inf3.3.4 One- and two-sided hypotheses
What is that mysterious last argument in fisher.test, alternative = "greater"? Well, there are three different sets of hypotheses that we may want to test:
- Whether the lady guesses better than random. Here \(H_0\): the lady’s guesses are no better than chance, and \(H_1\): the lady’s guesses are better than chance.
- Whether the lady guesses worse than random. Here \(H_0\): the lady’s guesses are no worse than chance, and \(H_1\): the lady’s guesses are worse than chance.
- Whether the lady’s guesses are either better than or worse than random. Here \(H_0\): the lady’s guesses are equally good as chance, and \(H_1\): the lady’s guesses are either worse than or better than chance.
The first two are said to be one-sided or directed, as they specify a direction in which the lady’s ability deviates from chance. The last set of hypotheses is said to be two-sided, because the lady’s abilities can deviate from chance in either direction. Because the alternative hypotheses are different, the three sets of hypotheses will yield different p-values (which is unsurprising, as we are asking different questions depending on how we specify our hypotheses).
Which of these we choose depends on what question we wish to answer. If, like Fisher, we want to know whether the lady has an uncanny ability to tell which cups were filled first with milk, we’d choose the first set of hypotheses. If instead we believe that maybe there is a difference in flavour that she can detect, but we’re not sure whether she can tell which is which, we may go with the third set instead.
We can change the alternative argument in fisher.test to use the three different sets of hypotheses as follows:
3.3.5 The lady binging tea: power and how the sample size affects the analysis
Fisher’s exact test can be used to illustrate an important principle: the greater the sample size, the easier it is to detect if \(H_1\) is true.
Let’s say that we wish to test whether the lady’s guesses are better than chance, using the significance level \(\alpha=0.05\). If she is served 2 cups where the milk was poured first and 2 where the tea was poured first, and guessed all of these correctly, we’d get the following result:
lady_results2 <- matrix(c(2, 0, 0, 2),
ncol = 2, nrow = 2,
byrow = TRUE,
dimnames = list(c("Guess: milk first", "Guess: tea first"),
c("Truth: milk first", "Truth: tea first")))
fisher.test(lady_results2, alternative = "greater")##
## Fisher's Exact Test for Count Data
##
## data: lady_results2
## p-value = 0.1667
## alternative hypothesis: true odds ratio is greater than 1
## 95 percent confidence interval:
## 0.357675 Inf
## sample estimates:
## odds ratio
## InfThe p-value is \(0.1667\), which is greater than \(\alpha\). Because the sample size is too small, we can’t reject \(H_0\) even when we get the most extreme outcome possible.
If we have a larger sample size, things are different. If the lady is served 15 cups where the milk was poured first and 15 where the tea was poured first, and guessed 11 of the cups where milked was poured first correctly, we’d get the following result:
lady_results2 <- matrix(c(11, 4, 4, 11),
ncol = 2, nrow = 2,
byrow = TRUE,
dimnames = list(c("Guess: milk first", "Guess: tea first"),
c("Truth: milk first", "Truth: tea first")))
fisher.test(lady_results2, alternative = "greater")##
## Fisher's Exact Test for Count Data
##
## data: lady_results2
## p-value = 0.01342
## alternative hypothesis: true odds ratio is greater than 1
## 95 percent confidence interval:
## 1.500179 Inf
## sample estimates:
## odds ratio
## 6.983892The p-value is \(0.01342\), which is smaller than \(\alpha\), and we can reject \(H_0\) even though the result was far from the most extreme outcome (which in this case would be 15 cups right).
What we’ve seen here is that it is easier to detect deviations from \(H_0\) when the sample size is larger.
The probability of rejecting \(H_0\) if \(H_1\) is true is called the power of the test. We want this to be as large as possible. The power will depend on the significance level \(\alpha\) (remember that this controls how strong evidence we need to reject \(H_0\)), how strong the effect is (it is easier to detect the lady’s ability if she gets 95% of all cups right than if she gets 55% of all cups right), and how large the sample size is. Generally, the power of a test increases when the sample size increases.
Clearly, the first experiment described above, with just 4 cups of tea, is a poorly designed one, as it never can lead to us rejecting \(H_0\). An important part of designing experiments is to perform power computations, where we calculate the power of the test under different scenarios and for different sample sizes. This lets us check how large a sample we need in order to obtain the desired power at a specific significance level \(\alpha\). We’ll see some examples of how this can be done later in this chapter as well as in Sections 7.2-7.3.
3.3.6 Permutation tests
In the lady tasting tea example, the lady was tasked with placing labels (milk first or tea first) on the cups. To compute the p-value, we calculated in how many ways she could do this, or how many permutations of the labels there were. We could then check how many of these permutations that yielded an outcome at least as extreme as that which we observed. A test based on permutations is called a permutation test. It is an important class of tests, which we will return to throughout the book.
Not all tests are permutation tests. Next, we’ll consider a different approach to testing hypotheses using contingency tables.
3.4 \(\chi^2\)-tests
When analysing a contingency table containing two variables \(X\) and \(Y\), there are two common types of tests. The first is a test of independence, where we test whether the two variables are independent:
- \(H_0\): the variables are independent; \(P(X=x \mbox{ and } Y=y)=P(X=x)P(Y=y)\) for all \(x,y\).
- \(H_1\): the variables are dependent; there is at least one pair \(x,y\) such that \(P(X=x \mbox{ and } Y=y)\neq P(X=x)P(Y=y)\).
The second is a test of homogeneity, where we test whether the distribution of \(Y\) is the same regardless of the value of \(X\), which in this case represents different populations:
- \(H_0\): the variables are independent; \(P(Y=y|X=x)=P(Y=y)\) for all \(x,y\).
- \(H_1\): the variables are dependent; there is at least one pair \(x,y\) such that \(P(Y=y|X=x)\neq P(Y=y)\).
Mathematically, a test of homogeneity is equivalent to a test of independence. The difference between the two lies in how the data is sampled. When we plan to perform a test of independence, we sample a single population and then break the observations down into the categories in the contingency table based on their \(X\) and \(Y\) values. When we plan to perform a test of homogeneity we instead sample several populations, corresponding to the levels of \(X\), and measure the value of \(Y\).
Finally, in some cases, we have a frequency table showing the distribution of a single variable. We may want to test whether this variable follows some specific distribution, \(F\), say. We then do a goodness-of-fit test of the hypotheses:
- \(H_0\): the variable follows the distribution \(F\).
- \(H_1\): the variable does not follow the distribution \(F\).
All three of these can be tested using a \(\chi^2\)-test (chi-squared test). Let’s say that \(X\) has \(c_x\) levels and that \(Y\) has \(c_y\) levels. Then for each of the \(c_x\cdot c_y\) cells in the table, we can compare the observed outcome \(o_{ij}\) to the outcome \(e_{ij}\) that would be expected if the null hypothesis were true. If the observed outcomes deviate a lot from what we would expect under the null hypothesis, we have evidence against \(H_0\).
Formally, the test is performed by computing the statistic
\[X^2=\sum_{i=1}^{c_x}\sum_{j=1}^{c_y}\frac{(o_{ij}-e_{ij})^2}{e_{ij}}.\] Large values of this statistic count as evidence against \(H_0\). It can be shown that under the null hypothesis, this statistic is asymptotically \(\chi^2\)-distributed, i.e., if the sample size is large enough, then the distribution of the statistic can be accurately approximated by the \(\chi^2\)-distribution. We can therefore compute the probability of obtaining an \(X^2\)-statistic that is larger than what we observed in our data, which gives us the p-value for the test.
This differs from Fisher’s exact test in that we rely on a mathematical approximation (the asymptotic \(\chi^2\)-distribution) rather than permutations when computing p-values. The benefit of this is speed: when the sample size becomes large, it takes a very long time to compute all possible permutations, whereas the \(X^2\)- statistic can be computed in milliseconds.
To run the test, we use the chisq.test function as follows:
If we wish to run a goodness-of-fit test, we specify the distribution \(F\) given by \(H_0\) using the argument p. If our null hypothesis is that both sexes are equally common, this would look as follows:
3.4.1 When can we use \(\chi^2\)-tests?
\(\chi^2\)-tests are approximate tests that require sufficiently large sample sizes to attain the right type I error rate. What is “large” is largely determined by how high the smallest expected cell counts are. A common rule-of-thumb is that the approximation is adequate as long as all \(e_{ij}>1\) and at most 20% of the cells have \(e_{ij}<5\) (Cochran, 1954).
To assess this, we can check the expected counts of the cells:
# Save the results of the test:
penguins |> select(species, sex) |> ftable() |> chisq.test() -> x2res
# Extract the expected counts:
x2res$expectedThe chisq.test output will also give a warning if any cells have \(e_{ij}<5\).
If your sample size is too small to use a \(\chi^2\) tests, there are two options in addition to gathering more data. The first is to merge some cells by merging levels of one or more of your categorical variables; see Section 5.4 for more on how this can be done. The second is to use simulated p-values, i.e., to use simulation rather than a mathematical approximation to compute the p-value. This turns the test into an approximate permutation test: the \(X^2\) statistic is computed for a large number of randomly selected permutations of the table, and the p-value is then computed as the proportion of permutations for which \(X^2\) was at least as large as for the original table. To use this approach, we add the argument simulate.p.value = TRUE to chisq.test. The argument B can also be added, to control how many permutations should be simulated; B = 9999 is a reasonable default choice.
Without pipes:
With pipes:
library(dplyr)
penguins |>
select(species, sex) |>
ftable() |>
chisq.test(simulate.p.value = TRUE, B = 9999)You’ll learn more about simulation in Chapter 7.
\[\sim\]
Exercise 3.1 In cases where our data is a contingency table rather than a data frame with one row for each observation, the simplest way to perform a \(\chi^2\)-test is to create a matrix object for the contingency table and run chisq.test with that as the input. Here is an example of such data, from a study on antibiotics resistance. In a lab, 18 strains of E.coli bacteria and 25 strains of K.pneumoniae bacteria were tested for resistance against an antibiotic. The table shows how many strains were resistant:
bacteria <- matrix(c(15, 3, 17, 8),
2, 2,
byrow = TRUE,
dimnames = list(c("E.coli", "K.pneumoniae"),
c("Not resistant", "Resistant")))Perform a \(\chi^2\) test of homogeneity to see if the proportion of resistant strains is the same for both species of bacteria. Are the conditions for running a \(\chi^2\)-test met? If not, what can you do instead?
(Click here to go to the solution.)
3.5 Confidence intervals
We use data to compute mean values, sample proportions, and other quantities. Almost always, our end goal is to draw some conclusion about a population parameter: the mean value in the underlying population, the proportion in the population, and so on.
Mean values and sample proportions give us estimates of the corresponding parameters in the population. But, how far off can the estimates be from the population parameters?
Confidence intervals are used to quantify the uncertainty of estimates and show what values of the population parameter are in agreement with the observed data.
Formally, a confidence interval for a parameter is an interval that will cover the true value of the parameter with probability \(1-\alpha\), where \(\alpha\) typically is \(0.05\), \(0.01\), or \(0.1\). \(1-\alpha\) is called the coverage or confidence level of the interval. The confidence level is a proportion but is frequently presented in percentages, i.e., as \((1-\alpha)\cdot 100 \%\). A confidence level of \(0.95\) or \(95 \%\) (i.e., with \(\alpha=0.05\)) means that the interval will cover the true value of the parameter in 95% of the studies where it is used.
Confidence intervals are much more informative than point estimates. Saying that the sample mean is 86.1 only tells part of the story. If we instead present a confidence interval, we also tell something about the uncertainty of this estimate. “The mean value is in the interval (85.9, 86.3) with 95% confidence” tells us that the uncertainty in the estimate is low, whereas “The mean value is in the interval (65.0, 107.2) with 95% confidence” tells us that the uncertainty is fairly high. In a way, reporting a confidence interval instead of just a point estimate is more honest, because it tells the whole story.
Like tests, confidence intervals can be either exact or approximate.
- For exact confidence intervals, the confidence level is at least \(1-\alpha\).
- For approximate confidence intervals, the confidence level is approximately \(1-\alpha\), but it may be lower than \(1-\alpha\).
The higher the confidence level, the wider the interval, because we need wider intervals if we want to be really sure that we cover the true value of the parameter. There is therefore a trade-off between having a confidence level that is high enough and an interval that isn’t so wide that it’s useless.
For any given parameter, there are different methods for computing a confidence interval. Some have better properties than others. We want an interval that has a coverage that is as close to \(1-\alpha\) as possible, but we also want it to be as short as possible. You’ll see examples of how statistical methods, including confidence intervals, can be evaluated in Section 7.2.
Confidence intervals and hypothesis tests are closely connected. For each test, the set of parameter values that wouldn’t be rejected if they were the null hypothesis, at significance level \(\alpha\), is a \(1-\alpha\) confidence interval. We will return to this connection in subsequent chapters.
3.5.1 Confidence intervals for proportions
As a first example, let’s consider confidence intervals for a proportion. We’ll use a function from the MKinfer package. Let’s install it:
The binomCI function in this package allows us to compute confidence intervals for proportions from binomial experiments using a number of methods. The input is the number of “successes” x, the sample size n, and the method to be used.
Let’s say that we want to compute a confidence interval for the proportion of herbivore mammals that sleep for more than 7 hours a day. First, we need to compute x and n.
Without pipes:
library(ggplot2)
herbivores <- msleep[msleep$vore == "herbi",]
# Compute the number of animals for which we know the sleep time:
n <- sum(!is.na(herbivores$sleep_total))
# Compute the number of "successes", i.e. the number of animals that sleep
# for more than 7 hours:
x <- sum(herbivores$sleep_total > 7, na.rm = TRUE)With pipes:
library(ggplot2)
library(dplyr)
# Compute the number of animals for which we know the sleep time and
# the number of "successes", i.e. the number of animals that sleep for
# more than 7 hours:
msleep |>
filter(vore == "herbi") |>
select(sleep_total) |>
na.omit() |>
summarise(n = n(),
x = sum(sleep_total > 7)) -> res
x <- res$x; n <- res$nThe estimated proportion is x/n, which in this case is 0.625. We’d like to quantify the uncertainty in this estimate by computing a confidence interval. The standard Wald method, taught in most introductory statistics courses, can be computed in the following way:
The confidence interval is printed on the line starting with prob: in this case, it is \((0.457, 0.792)\).
Don’t use that method though! The Wald interval is known to be severely flawed (Brown et al., 2001), primarily because its coverage can be very far from \(1-\alpha\). Much better options are available. If the proportion can be expected to be close to 0 or 1, the Clopper-Pearson interval is recommended, and otherwise the Wilson interval is the best choice (Thulin, 2014a). We can use either of these methods with binomCI:
binomCI(x, n, conf.level = 0.95, method = "clopper-pearson")
binomCI(x, n, conf.level = 0.95, method = "wilson")\[\sim\]
Exercise 3.2 In a survey, 440 out of 998 randomly sampled respondents said that they plan to vote for a particular candidate in an upcoming election. Based on this, compute a 99% Wilson interval for the proportion of voters that plan to vote for this candidate.
(Click here to go to the solution.)
Exercise 3.3 The function binomDiffCI from MKinfer can be used to compute a confidence interval for the difference of two proportions. Using the msleep data, use it to compute a confidence interval for the difference between the proportion of herbivores that sleep for more than 7 hours a day and the proportion of carnivores that sleep for more than 7 hours a day.
3.5.2 Sample size calculations
Confidence intervals that are too wide aren’t that informative. We’d much rather be able to say “the proportion is somewhere between 0.56 and 0.58” than “the proportion is somewhere between 0.37 and 0.78”.
How wide a confidence interval for a proportion is depends both on the number of successes \(x\) and the sample size \(n\). We don’t know \(x\) in advance but can usually control \(n\), at least to some extent. It is therefore often useful to perform some computations prior to collecting our data, to make sure that \(n\) is large enough that we’ll get a confidence interval with a reasonable width.
The MKpower package contains several functions that will prove useful when we wish to calculate what sample size we need for a study. Let’s install it:
The ssize.propCI function in MKpower can be used to compute the sample size needed to obtain a confidence interval with a given width – or rather, a given expected, or average, width. The width of the interval is a function of a random variable and is therefore also random. The computations rely on asymptotic formulas that are highly accurate, as you later will verify in Exercise 7.9.
When computing the required sample size, we give a rough approximation of what we expect the proportion to be (prop), and specify what width we want our confidence interval to be (width):
library(MKpower)
# Compute the sample size required to obtain an interval with
# width 0.1 if the true proportion is 0.4:
ssize.propCI(prop = 0.4, width = 0.1,
conf.level = 0.95, method = "wilson")
ssize.propCI(prop = 0.4, width = 0.1,
conf.level = 0.95, method = "clopper-pearson")In the output from these function calls, n is the sample size required to obtain the desired expected width. Try lowering the desired width and see how that effects the required sample size.
\[\sim\]
Exercise 3.4 What sample size is required to obtain a 95% Wilson confidence interval with expected width 0.05 if the true proportion is 0.7?
3.6 Comparing mean values
In Section 3.3 we imagined a study where we wanted to find out whether flipper length differs between male and female Chinstrap penguins. The penguins dataset can be used for this purpose. It contains measurements of the flipper lengths of a number of penguins. If the average length in the female population is \(\mu_1\) and the average length in the male population is \(\mu_2\), then the population parameter that we are interested in is the difference \(\mu_1-\mu_2\). The hypotheses that we wish to test are:
- \(H_0\): there is no difference; \(\mu_1-\mu_2=0\).
- \(H_1\): there is a difference; \(\mu_1-\mu_2 \neq 0\).
In this section, we will learn about the t-test, which can be used to test this and similar hypotheses about means and differences of means. Throughout the section, we’ll assume that all observations are independent, unless we explicitly say that they aren’t.
3.6.1 The t-test for comparing two groups
It seems reasonable to base a test of these hypotheses on the difference between the sample means in the two samples: \(\bar{x}_1-\bar{x}_2\). There is one problem though: said difference is not scale invariant, and so we would get different results depending on whether we measure the flipper lengths in centimetres, metres, or inches. To remedy that, we base our test on the quantity
\[T=\frac{\bar{x}_1-\bar{x}_2}{s}\]
where \(s\) is the standard error of \(\bar{x}_1-\bar{x}_2\) (i.e., an estimate of the standard deviation of the mean difference). How the latter is computed depends on what assumptions we are willing to make. The test based on \(T\) is called the two-sample t-test. There are two different versions of this test, which differ in how \(s\) is computed:
- The equal-variances t-test: where the variance is assumed to be the same in both populations.
- The Welch t-test: where the variance is allowed to differ between the two populations.
The equal-variances t-test will not work properly when the two populations have differing variances – a low p-value may be due to differences in variances rather than differences in means. In such cases, it no longer tests the hypotheses we were interested in; instead, it tests whether the distribution is the same for the two populations. If that is the question that you’re interested in, there are other, better, tests that you can use instead, such as the Kolmogorov-Smirnov test, implemented in ks.test.
The Welch t-test works well both when the population variances differ and when they are equal, and it tests the right hypotheses in both cases. It is the default in R, and I strongly recommend using it instead of the equal-variances test. Some textbooks recommend first performing a test to see whether the population variances differ, and then using that to choose which version of the t-test to use. This is a widespread practice. Indeed, software packages such as SAS and SPSS include such tests in the default output for the t-test. While it may sound like a good idea, this actually leads to a procedure that generally performs worse than the Welch t-test (Rasch et al., 2011; Delacre et al., 2017).
In summary, forget about different versions of the two-sample t-test, and always use the Welch t-test. As it is the default in R, this is easy to do! Here is an example of how to perform a Welch t-test to test whether flipper length differs between male and female Chinstrap penguins, using the t.test function:
In the solution using pipes, recall that data = _ means that the data used is the output from the previous step in the pipeline (see Section 2.13.2).
The output looks as follows:
##
## Welch Two Sample t-test
##
## data: flipper_length_mm by sex
## t = -5.7467, df = 65.905, p-value = 0.0000002535
## alternative hypothesis: true difference in means between group female and group male
## is not equal to 0
## 95 percent confidence interval:
## -11.017272 -5.335669
## sample estimates:
## mean in group female mean in group male
## 191.7353 199.9118We are mostly interested in the p-value, which in this case is very low, leading us to reject \(H_0\) and conclude that there is a difference.
In addition to the p-value, a 95% confidence interval for the difference \(\mu_1-\mu_2\) is also presented (remember that there is a close connection between confidence intervals and hypothesis test), along with the means in the two groups. The confidence interval is \((-11.0, -5.3)\), meaning that the average flipper length in females is somewhere between \(5.3\) and \(11.0\) mm shorter than in males.
\[\sim\]
Exercise 3.5 Consider the penguins data again. Run a t-test to see if the average body mass differs between the sexes for Chinstrap penguins.
3.6.2 One-sided hypotheses
The t-test can also be used to test directed hypotheses, such as:
- \(H_0\): \(\mu_1-\mu_2\geq 0\).
- \(H_1\): \(\mu_1-\mu_2 < 0\).
To specify that a one-sided test should be performed, we use the alternative argument, just as we did for Fisher’s exact test in Section 3.3.4:
3.6.3 The t-test for a single sample
In some cases, we wish to test hypotheses about the mean value of a single population. For example:
- \(H_0\): the mean value equals some specific value \(\mu_0\); \(\mu=\mu_0\).
- \(H_1\): the mean value does not equal \(\mu_0\); \(\mu\neq\mu_0\).
This can be done using a one-sample t-test, which uses a test statistic based on the sample mean \(\bar{x}\). We use t.test and specify the value \(\mu_0\) of \(\mu\) under \(H_0\) using the argument mu. Here’s an example where we test whether the average length of the flippers of male Chinstrap penguins is 200 mm:
Without pipes:
library(palmerpenguins)
t.test(flipper_length_mm ~ 1,
data = subset(penguins, species == "Chinstrap" & sex == "male"),
mu = 200)
# Or, in two steps:
new_data <- penguins[penguins$species == "Chinstrap" & penguins$sex == "male",]
t.test(new_data$flipper_length_mm, mu = 200)With pipes:
library(palmerpenguins)
library(dplyr)
penguins |>
filter(species == "Chinstrap", sex == "male") |>
t.test(flipper_length_mm ~ 1, data = _, mu = 200)In this case, the p-value is 0.93 and we cannot reject \(H_0\) – that is, we do not have any statistical evidence that the average flipper length isn’t 200 mm.
\[\sim\]
Exercise 3.6 Consider the penguins data again. Run a one-sided test to see if the average flipper length for male Chinstrap penguins is greater than 195.
3.6.4 The t-test for paired samples
In some cases, we have paired observations in our data, i.e., observations that have been collected in pairs. A common example is when we make measurements on the same subjects before and after a treatment. In such situations, we are often interested in the effect \(\Delta\) of the treatment, where \(\Delta\) measures how much the mean value changes because of the treatment. A common set of hypotheses are:
- \(H_0\): there is no effect; \(\Delta=0\).
- \(H_1\): there is an effect; \(\Delta \neq 0\).
These can be tested using a paired samples t-test, where the two samples (before and after) are compared using the information about the pairing. Here is an example with measurements before and after a treatment stored in different columns in a table:
exdata <- data.frame(before = c(8.5, 4.4, 9.4, 0.0, 2.2, 9.7, 6.2, 8.2),
after = c(8.5, 4.8, 10.1, 1.0, 5.6, 11.4, 7.8, 10.2))We could run a two-sample t-test to compare the two samples, but that would result in a test with lower power, as it ignores some of the information available to use (namely that the observations belong in pairs). A paired samples t-test is always preferable when you have paired data.
3.6.5 When can we use the t-test?
The first requirements for the t-test to work is that the observations are independent. The only exception to this is when we have paired samples, in which case we allow the observations within a pair to be dependent. Dependence between observations occur for instance when we have multiple observations for the same individual. Methods for analysing such datasets are discussed in Section 8.8.
And then there is the matter of the normal distribution.
For decades teachers all over the world have been telling the story of William Sealy Gosset: the head brewer at Guinness who derived the formulas used for the t-test and, following company policy, published the results under the pseudonym “Student”. By assuming that the variable followed a normal distribution, he was able to derive the distribution of the \(t\)-statistic under the null distribution, which could then be used to compute p-values.
The tests (and the associated confidence intervals) described above work well when the variables we are interested in indeed do follow a normal distribution. For the two-sample test, the variable should be normal in each population. For the paired samples test, the differences need to follow a normal distribution.
Unfortunately, real data is almost never normally distributed.
If the variable doesn’t follow a normal distribution (you’ll learn more about assessing the normality assumption in Section 7.1.3), the tests and confidence intervals may still be valid if you have large sample sizes, or, for the two-sample test, if you have balanced sample sizes, i.e., equally many observations in each group. How large “large” is depends on the shape of the distribution. The less symmetric it is, the larger the sample size needs to be.
But, why do we need the normality assumption in the first place? Is there some way that we can get rid of it? It turns out that there is. Gosset’s work was hugely important, but the passing of time has rendered at least parts of it largely obsolete. His distributional formulas were derived out of necessity: lacking the computer power that we have available to us today, he was forced to impose the assumption of normality on the data, in order to derive the formulas he needed to be able to carry out his analyses. Today we can use simulation to carry out analyses with fewer assumptions. As an added bonus, these simulation techniques often happen to result in statistical methods with better performance than Student’s t-test and other similar methods. You’ll learn about two simulation-based ways to compute p-values for the t-test next.
3.6.6 Permutation t-tests
Continuing our example with the Chinstrap penguin data, we note that there are 34 males and 34 females in the sample – 68 animals in total. If there are no differences in flipper length between the sexes (i.e., if \(H_0\) is true), the sex labels offer no information about how long the flippers are. Under the null hypothesis, the assignment of sex labels to different animals is therefore for all intents and purposes random. To find the distribution of the test statistic under the null hypothesis, we could look at all possible ways to assign 34 animals the label male and 34 animals the label female. That is, look at all permutations of the labels. The probability of a result at least as extreme as that obtained in our sample (in the direction of the alternative), i.e., the p-value, would then be the proportion of permutations that yield a \(t\)-statistic at least as extreme as that in our sample.
This is a permutation version of the \(t\)-test. Note that it doesn’t rely on any assumptions about normality.
Permutation tests were known to the statisticians that developed the t-test in the first decades of the 20th century, but because the number of permutations of labels often tend to become quite large (28,453,041,475,240,599,552, in our male–female example), they lacked the means to actually use them, and so had to resort to cruder mathematical approximations using assumptions about the distribution of the data. The 28,453,041,475,240,599,552 permutations may be too many even today, but we can obtain very good approximations of the p-values of permutation tests using simulation.
The idea is that we look at a large number of randomly selected permutations, and check for how many of them we obtain a test statistic that is more extreme than the sample test statistic. The law of large numbers guarantees that this proportion will converge to the permutation test p-value as the number of randomly selected permutations increases.
The function that we’ll use to perform a simulation-based permutation t-test, perm.t.test, works exactly like t.test. In all the examples above, we can replace t.test with perm.t.test to run a (simulation-based) permutation t-test instead. Here’s how to do it:
Note that two p-values and confidence intervals are presented: one set from the permutations and one from the traditional approach – so make sure that you look at the right ones!
So, you say, how many randomly selected permutations do we need to get an accurate approximation of the permutation test p-value? My answer is that, by default, perm.t.test uses 9,999 permutations (you can change that number using the argument R), which is widely considered to be a reasonable number. If you are running a permutation test with a much more complex (and computationally intensive) statistic, you may have to use a lower number, but avoid that if you can.
You may ask why we use 9,999 permutations and not 10,000. The reason is that we avoid p-values that are equal to traditional significance levels like 0.05 and 0.01 this way. If we’d used 10,000 permutations, 500 of which yielded a statistics that had a larger absolute value than the sample statistic, then the p-value would have been exactly 0.05, which would cause some difficulties in trying to determine whether or not the result was significant at the 5% level. This cannot happen when we use 9,999 permutations instead (500 statistics with a large absolute value yields the p-value \(0.050005>0.05\), and 499 yields the p-value \(0.0499<0.05\)).
3.6.7 Bootstrap t-tests
A popular method for computing p-values and confidence intervals that resembles the permutation approach is the bootstrap. Instead of drawing permuted samples, new observations are drawn with replacement from the original sample, and then labels are randomly allocated to them. That means that each randomly drawn sample will differ not only in the permutation of labels, but also in what observations are included – some may appear more than once and some not at all. We can then check what proportion of these bootstrap samples that yield a more extreme test statistic than what we observed in our original sample. In effect, the p-value is computed in the same way as in the traditional t-test, but with the theoretical normal distribution replaced with the empirical distribution of the data. We can therefore view the bootstrap t-test as a compromise between the traditional t-test and the permutation t-test.
We will have a closer look at the bootstrap in Section 7.4, where we will learn how to use it for creating confidence intervals and computing p-values for any test statistic. For now, we’ll just note that MKinfer offers a bootstrap version of the t-test, boot.t.test :
Both perm.test and boot.test have a useful argument called symmetric, the details of which are discussed in depth in Section 14.3.
3.6.8 Publication-ready tables for means
In Section 3.2.2, we used tbl_summary from the gtsummary package to create summary tables for categorical variables. It can also be used for numeric variables. In the example below, we create a table showing the average flipper length for male and female Chinstrap penguins.
By default, tbl_summary displays the median and inter-quartile range for numeric variables:
library(palmerpenguins)
library(dplyr)
library(gtsummary)
penguins |>
filter(species == "Chinstrap") |>
select(sex, flipper_length_mm) |>
tbl_summary(by = sex)We can however change this, and for instance print the mean value and bootstrap confidence intervals instead. This involves creating custom functions, a topic which you’ll learn more about in Section 6.1. For now, we’ll just use the first two lines of the code chunk below without fully understanding why they work (the first line creates a function that extracts the lower confidence bound, and the second line creates a function that extracts the upper confidence bound), to obtain a table showing what we want:
confint1 <- function(x) { MKinfer::boot.t.test(x)$boot.conf.int[1] }
confint2 <- function(x) { MKinfer::boot.t.test(x)$boot.conf.int[2] }
penguins |>
filter(species == "Chinstrap") |>
select(sex, flipper_length_mm) |>
tbl_summary(by = sex, statistic = list(
all_continuous() ~ "{mean} ({confint1}, {confint2})",
all_categorical() ~ "{n} ({p}%)"))To export the output from t.test to a nice-looking table, we can use tbl_regression:
3.6.9 Sample size computations for the t-test
In any study, it is important to collect enough data for the inference that we wish to make. If we want to use a t-test for a test about a mean or the difference of two means, what constitutes “enough data” is usually measured by the power of the test. The sample is large enough when the test achieves high enough power. If we are comfortable assuming normality (and we may well be, especially as the main goal with sample size computations is to get a ballpark figure), we can use power.t.test to compute what power our test would achieve under different settings. For a two-sample test with unequal variances, we can use power.welch.t.test from MKpower instead. Both functions can be used to either find the sample size required for a certain power, or to find out what power will be obtained from a given sample size.
power.t.test and power.welch.t.test both use delta to denote the mean difference under the alternative hypothesis. In addition, we must supply the standard deviation sd of the distribution. Here are some examples:
library(MKpower)
# A one-sided one-sample test with 80 % power:
power.t.test(power = 0.8, delta = 1, sd = 1, sig.level = 0.05,
type = "one.sample", alternative = "one.sided")
# A two-sided two-sample test with sample size n = 25 and equal
# variances:
power.t.test(n = 25, delta = 1, sd = 1, sig.level = 0.05,
type = "two.sample", alternative = "two.sided")
# A one-sided two-sample test with 90 % power and equal variances:
power.t.test(power = 0.9, delta = 1, sd = 0.5, sig.level = 0.01,
type = "two.sample", alternative = "one.sided")
# A one-sided two-sample test with 90 % power and unequal variances:
power.welch.t.test(power = 0.9, delta = 1, sd1 = 0.5, sd2 = 1,
sig.level = 0.01,
alternative = "one.sided")You may wonder how to choose delta and sd. If possible, it is good to base these numbers on a pilot study or related previous work. If no such data is available, your guess is as good as mine. For delta, some useful terminology comes from medical statistics, where the concept of clinical significance is used increasingly often. Make sure that delta is large enough to be clinically significant, that is, large enough to actually matter in practice.
If we have reason to believe that the data follows a non-normal distribution, another option is to use simulation to compute the sample size that will be required. We’ll do just that in Section 7.3.
\[\sim\]
Exercise 3.7 Return to the one-sided t-test that you performed in Exercise 3.6. Assume that delta is 5 (i.e., that the true mean is 200) and that the standard deviation is 6. How large does the sample size \(n\) have to be for the power of the test to be 95% at a 5% significance level? What is the power of the test when the sample size is \(n=34\) (which is the case for the penguins data)?
3.7 Multiple testing
If we run a single hypothesis test, the risk for a type I error (also called a false positive result) is \(\alpha\). If we run two independent tests, the risk for committing at least one type I error is greater, as there now are two tests for which this can occur. When we run even more tests, the risk for a type I error increases, to the point where we’re virtually guaranteed to get at least one significant result, even if the null hypotheses are true for all tests.
The figure below shows the risk of getting at least one type I error when we perform multiple independent tests for which the null hypothesis is true. As you can see, the risk quickly becomes quite high.
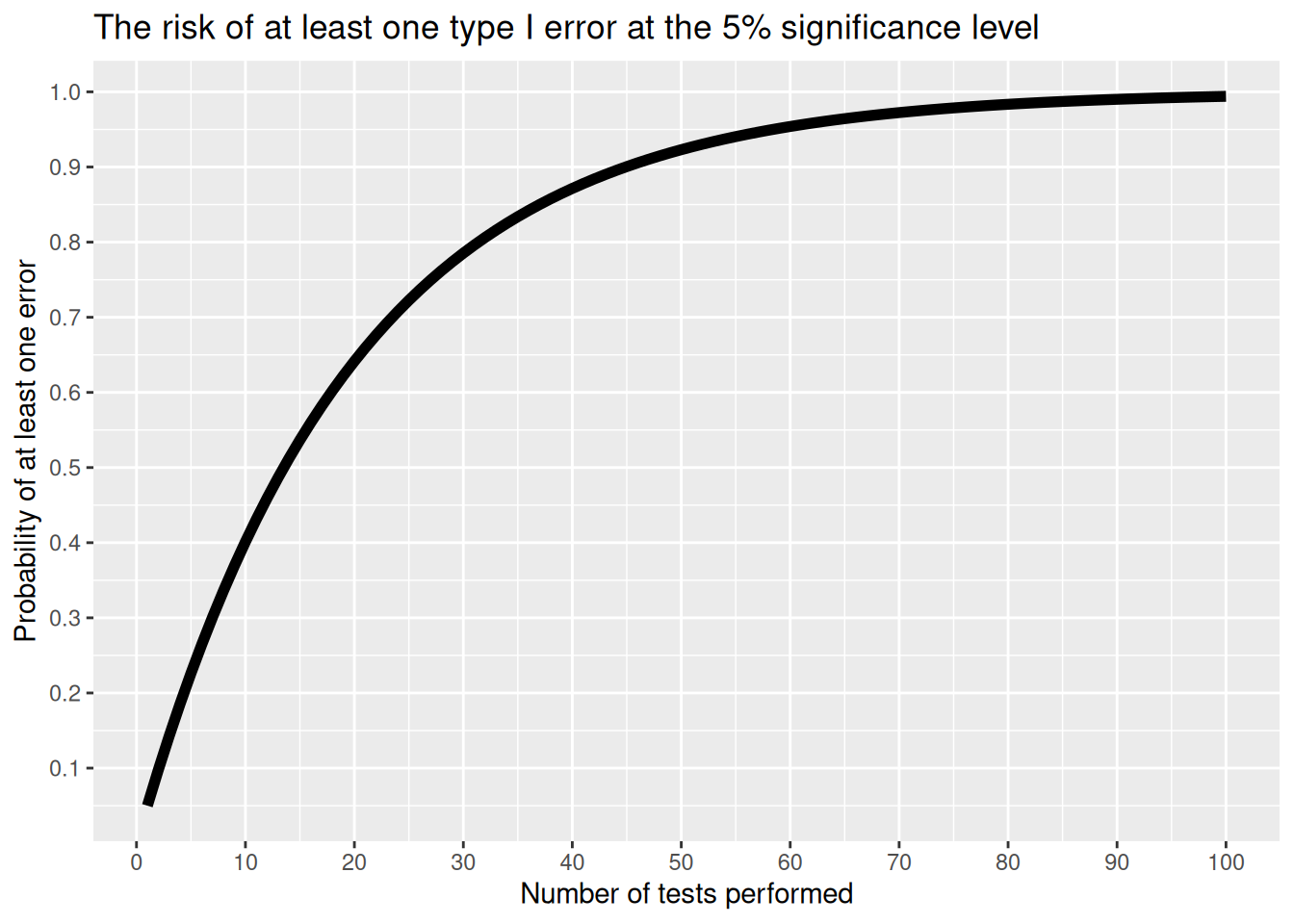
Figure 3.1: The risk of at least one type I error when performing multiple tests.
3.7.1 Adjusting for multiplicity
We can reduce the risk of false positive results by adjusting the p-values of the tests for multiplicity. When this is done, the p-values are increased somewhat, to decrease the risk of type I errors.
There are severals methods for adjusting for multiplicity, including for instance Bonferroni correction (a method that often is too conservative and adjusts the p-values too much), Holm’s method (an improved version of the standard Bonferroni approach), and the Benjamini-Hochberg approach (which controls the false discovery rate and is useful if you for instance are screening a lot of variables for differences).
We can apply these methods by using p.adjust:
# Some example p-values:
p_values <- c(0.00023, 0.003, 0.021, 0.042, 0.060, 0.2, 0.81)
# Adjusted p-values:
p.adjust(p_values, method = "bonferroni")
p.adjust(p_values, method = "holm")
p.adjust(p_values, method = "BH")The adjusted p-values are then compared to \(\alpha\). If the Bonferroni or Holm methods have been used, the probability of at least one type I error is bounded by \(\alpha\) under certain assumptions.
\[\sim\]
Exercise 3.8 Rerun the test from Exercise 3.5, once for each penguin species in the penguins data. Are the null hypotheses rejected? If so, are the differences still significant after adjusting for multiplicity using Holm’s method?
Hint: you can extract the p-values from the t.test function using t.test(...)$p.val (replace ... with the usual arguments).
3.7.2 Multivariate testing with Hotelling’s \(T^2\)
If you are interested in comparing the means of several variables for two groups, using a multivariate test is sometimes a better option than running multiple univariate t-tests. The multivariate generalisation of the t-test, Hotelling’s \(T^2\), is available through the Hotelling package:
As an example, consider the airquality data. Let’s say that we want to test whether the mean ozone, solar radiation, wind speed, and temperature differ between June and July. We could use four separate t-tests to test this, but we could also use Hotelling’s \(T^2\) to test the null hypothesis that the mean vector, i.e., the vector containing the four means, is the same for both months. The function used for this is hotelling.test:
# Subset the data:
airquality_t2 <- subset(airquality, Month == 6 | Month == 7)
# Run the test under the assumption of normality:
library(Hotelling)
t2 <- hotelling.test(Ozone + Solar.R + Wind + Temp ~ Month,
data = airquality_t2)
t2
# Run a permutation test instead:
t2 <- hotelling.test(Ozone + Solar.R + Wind + Temp ~ Month,
data = airquality_t2, perm = TRUE)
t23.8 Correlations
We are often interested in measuring how strong the dependence between two variables is. A common group of such measures are called correlation measures. A correlation measure ranges from -1 (perfect negative dependence) to 1 (perfect positive dependence), with 0 meaning that there is no dependence (in the sense measured by the correlation measure). Values close to 1 indicate strong positive dependence, and values close to -1 indicate strong negative dependence.
3.8.1 Estimation
The most commonly used correlation measure is the Pearson correlation. It measures how strong the linear dependence is between two variables. This means that the correlation can be close to 0 even if there is a dependence, as long as that dependence is non-linear:
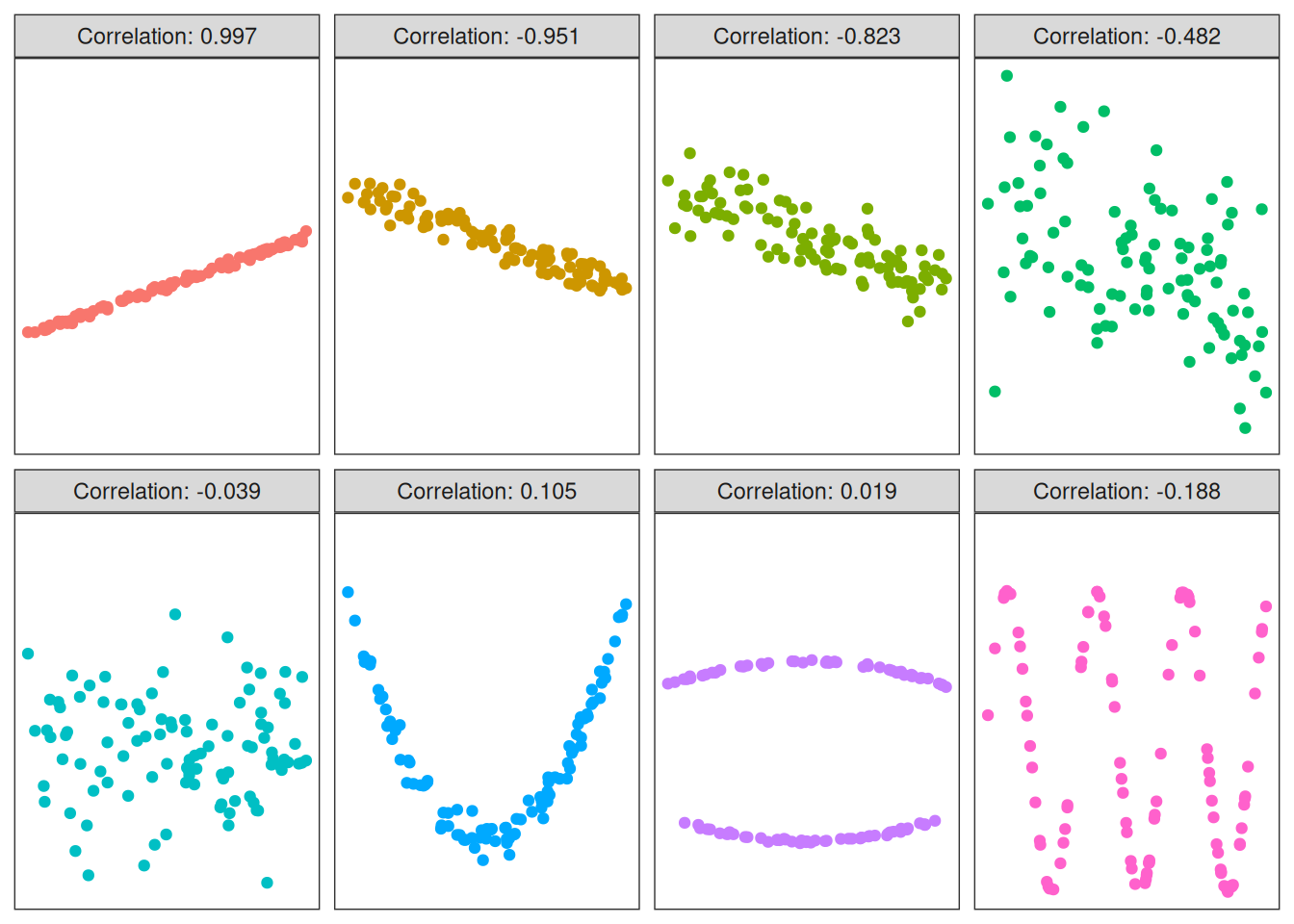
Figure 3.2: The Pearson correlation for eight datasets.
We can compute the Pearson correlation between two variables using cor:
The setting use = "pairwise.complete" means that NA values are ignored.
The result, a correlation of 0.87, indicates a fairly strong linear dependence between the two variables.
Another common option is the Spearman correlation, which measures the strength of monotone dependence between two variables. This means that it’s better at finding non-linear dependencies.
In this case, the two methods yield similar results.
3.8.2 Hypothesis testing
To test the null hypothesis that two numerical variables are uncorrelated, i.e., that their correlation is 0, we can use cor.test. The test can be based on either the Pearson correlation (the default) or the Spearman correlation.
Let’s try it with sleep times and brain weight, using the msleep data again:
library(ggplot2)
# Pearson correlation
cor.test(msleep$sleep_total, msleep$brainwt,
use = "pairwise.complete")
# Spearman correlation
cor.test(msleep$sleep_total, msleep$brainwt,
method = "spearman",
use = "pairwise.complete")These tests are all based on asymptotic approximations, which among other things cause the Pearson correlation test to perform poorly for non-normal data. In Section 7.4 we will create a bootstrap version of the correlation test, which has better performance.
3.9 Bayesian approaches
The Bayesian paradigm differs in many ways from the frequentist approach that we use in the rest of this chapter. In Bayesian statistics, we first define a prior distribution for the parameters that we are interested in, representing our beliefs about them (for instance based on previous studies). Bayes’ theorem is then used to derive the posterior distribution, i.e., the distribution of the coefficients given the prior distribution and the data. Philosophically, this is very different from frequentist estimation, in which we don’t incorporate prior beliefs into our models (except for through what variables we include).
In many situations, we don’t have access to data that can be used to create an informative prior distribution. In such cases, we can use a so-called weakly informative prior instead. These act as a sort of “default priors”, representing large uncertainty about the values of the coefficients.
The rstanarm package contains methods for using Bayesian estimation to fit some common statistical models. It takes a while to install but is well worth the wait:
3.9.1 Inference for a proportion
Let’s return to the example that we used in Section 3.5.1:
library(ggplot2)
herbivores <- msleep[msleep$vore == "herbi",]
# Compute the number of animals for which we know the sleep time:
n <- sum(!is.na(herbivores$sleep_total))
# Compute the number of "successes", i.e. the number of animals
# that sleep for more than 7 hours:
x <- sum(herbivores$sleep_total > 7, na.rm = TRUE)The Bayesian analogue to a confidence interval is a credible interval: an interval that covers the population parameter with a posterior probability that is \(1-\alpha\).
An excellent Bayesian credible interval for a proportion is the Jeffreys interval, which uses the weakly informative Jeffreys prior:
The Jeffreys interval is interesting because it also has good frequentist properties (Brown et al., 2001).
3.9.2 Inference for means
To use a Bayesian model with a weakly informative prior to analyse the difference in sleep time between herbivores and carnivores, we load rstanarm and use stan_glm in complete analogue with how we use t.test:
library(rstanarm)
library(ggplot2)
m <- stan_glm(sleep_total ~ vore, data =
subset(msleep, vore == "carni" | vore == "herbi"))
# Print the estimates:
mThere are two estimates here: an “intercept” (the average sleep time for carnivores) and voreherbi (the difference between carnivores and herbivores). To plot the posterior distribution of the difference, we can use plot:
To get a 95% credible interval for the difference, we can use posterior_interval as follows:
p-values are not a part of Bayesian statistics, so don’t expect any. It is however possible to perform a kind of Bayesian test of whether there is a difference by checking whether the credible interval for the difference contains 0. If not, we have evidence that there is a difference (Thulin, 2014c). In this case, 0 is contained in the interval, and there is no evidence of a difference.
In most cases, Bayesian estimation is done using Monte Carlo integration (specifically, a class of methods known as Markov Chain Monte Carlo, MCMC). To check that the model fitting has converged, we can use a measure called \(\hat{R}\). It should be less than 1.1 if the fitting has converged:
If the model fitting hasn’t converged, you may need to increase the number of iterations of the MCMC algorithm. You can increase the number of iterations by adding the argument iter to stan_glm (the default is 2,000).
If you want to use a custom prior for your analysis, that is of course possible too. See ?priors and ?stan_glm for details about this, and about the default weakly informative prior.
3.10 Reporting statistical results
Carrying out a statistical analysis is only the first step. After that, you probably need to communicate your results to others: your boss, your colleagues, your clients, the public, and so on. This section contains some tips for how best to do that.
3.10.1 What should you include?
When reporting your results, it should always be clear:
- How the data was collected,
- If, how, and why any observations were removed from the data prior to the analysis,
- What method was used for the analysis (including a reference unless it is a routine method),
- If any other analyses were performed/attempted on the data, and if you don’t report their results, why.
Let’s say that you’ve estimated some parameter, for instance the mean sleep time of mammals, and want to report the results. The first thing to think about is that you shouldn’t include too many decimals: don’t give the mean with 5 decimals if sleep times only were measured with one decimal.
BAD: The mean sleep time of mammals was found to be 10.43373.
GOOD: The mean sleep time of mammals was found to be 10.4.
It is common to see estimates reported with standard errors or standard deviations:
BAD: The mean sleep time of mammals was found to be 10.3 (\(\sigma=4.5\)).
or
BAD: The mean sleep time of mammals was found to be 10.3 (standard error 0.49).
or
BAD: The mean sleep time of mammals was found to be \(10.3 \pm 0.49\).
Although common, this isn’t a very good practice. Standard errors/deviations are included to give some indication of the uncertainty of the estimate but are very difficult to interpret. In most cases, they will probably cause the reader to either overestimate or underestimate the uncertainty in your estimate. A much better option is to present the estimate with a confidence interval, which quantifies the uncertainty in the estimate in an interpretable manner:
GOOD: The mean sleep time of mammals was found to be 10.3 (95% percentile bootstrap confidence interval: 9.5-11.4).
Similarly, it is common to include error bars representing standard deviations and standard errors, e.g., in bar charts. This questionable practice becomes even more troublesome because a lot of people fail to indicate what the error bars represent. If you wish to include error bars in your figures, they should always represent confidence intervals, unless you have a very strong reason for them to represent something else. In the latter case, make sure that you clearly explain what the error bars represent.
If the purpose of your study is to describe differences between groups, you should present a confidence interval for the difference between the groups, rather than one confidence interval (or error bar) for each group. It is possible for the individual confidence intervals to overlap even if there is a significant difference between the two groups, so reporting group-wise confidence intervals will only lead to confusion. If you are interested in the difference, then of course the difference is what you should report a confidence interval for.
BAD: There was no significant difference between the sleep times of carnivores (mean 10.4, 95% percentile bootstrap confidence interval: 8.4-12.5) and herbivores (mean 9.5, 95% percentile bootstrap confidence interval: 8.1-12.6).
GOOD: There was no significant difference between the sleep times of carnivores (mean 10.4) and herbivores (mean 9.5), with the 95% percentile bootstrap confidence interval for the difference being (-1.8, 3.5).
3.10.2 Citing R packages
In statistical reports, it is often a good idea to specify what version of a software or a package you used, for the sake of reproducibility (indeed, this is a requirement in some scientific journals). To get the citation information for the version of R that you are running, simply type citation(). To get the version number, you can use R.Version as follows:
To get the citation and version information for a package, use citation and packageVersion as follows:
3.11 Ethics and good statistical practice
Throughout this book, there will be sections devoted to ethics. Good statistical practice is intertwined with good ethical practice. Both require transparent assumptions, reproducible results, and valid interpretations.
3.11.1 Ethical guidelines
One of the most commonly cited ethical guidelines for statistical work is The American Statistical Association’s (ASA) Ethical Guidelines for Statistical Practice (Committee on Professional Ethics of the American Statistical Association, 2018), a shortened version of which is presented below22. The full ethical guidelines are available at: https://www.amstat.org/ASA/Your-Career/Ethical-Guidelines-for-Statistical-Practice.aspx
- Professional Integrity and Accountability. The ethical statistician uses methodology and data that are relevant and appropriate; without favoritism or prejudice; and in a manner intended to produce valid, interpretable, and reproducible results. The ethical statistician does not knowingly accept work for which he/she is not sufficiently qualified, is honest with the client about any limitation of expertise, and consults other statisticians when necessary or in doubt. It is essential that statisticians treat others with respect.
- Integrity of Data and Methods. The ethical statistician is candid about any known or suspected limitations, defects, or biases in the data that may affect the integrity or reliability of the statistical analysis. Objective and valid interpretation of the results requires that the underlying analysis recognises and acknowledges the degree of reliability and integrity of the data.
- Responsibilities to Science/Public/Funder/Client. The ethical statistician supports valid inferences, transparency, and good science in general, keeping the interests of the public, funder, client, or customer in mind (as well as professional colleagues, patients, the public, and the scientific community).
- Responsibilities to Research Subjects. The ethical statistician protects and respects the rights and interests of human and animal subjects at all stages of their involvement in a project. This includes respondents to the census or to surveys, those whose data are contained in administrative records, and subjects of physically or psychologically invasive research.
- Responsibilities to Research Team Colleagues. Science and statistical practice are often conducted in teams made up of professionals with different professional standards. The statistician must know how to work ethically in this environment.
- Responsibilities to Other Statisticians or Statistics Practitioners. The practice of statistics requires consideration of the entire range of possible explanations for observed phenomena, and distinct observers drawing on their own unique sets of experiences can arrive at different and potentially diverging judgments about the plausibility of different explanations. Even in adversarial settings, discourse tends to be most successful when statisticians treat one another with mutual respect and focus on scientific principles, methodology, and the substance of data interpretations.
- Responsibilities Regarding Allegations of Misconduct. The ethical statistician understands the differences between questionable statistical, scientific, or professional practices and practices that constitute misconduct. The ethical statistician avoids all of the above and knows how each should be handled.
- Responsibilities of Employers, Including Organizations, Individuals, Attorneys, or Other Clients Employing Statistical Practitioners. Those employing any person to analyse data are implicitly relying on the profession’s reputation for objectivity. However, this creates an obligation on the part of the employer to understand and respect statisticians’ obligation of objectivity.
Similar ethical guidelines for statisticians have been put forward by the International Statistical Institute (https://www.isi-web.org/about-isi/policies/professional-ethics), the United Nations Statistics Division (https://unstats.un.org/unsd/dnss/gp/fundprinciples.aspx), and the Data Science Association (http://www.datascienceassn.org/code-of-conduct.html). For further reading on ethics in statistics, see Franks (2020) and Fleming & Bruce (2021).
\[\sim\]
Exercise 3.9 Discuss the following. In the introduction to American Statistical Association’s Ethical Guidelines for Statistical Practice, it is stated that “using statistics in pursuit of unethical ends is inherently unethical”. What is considered unethical depends on social, moral, political, and religious values, and ultimately you must decide for yourself what you consider to be unethical ends. Which (if any) of the following do you consider to be unethical?
- Using statistical analysis to help a company that harm the environment through their production processes. Does it matter to you what the purpose of the analysis is?
- Using statistical analysis to help a tobacco or liquor manufacturing company. Does it matter to you what the purpose of the analysis is?
- Using statistical analysis to help a bank identify which loan applicants that are likely to default on their loans.
- Using statistical analysis of social media profiles to identify terrorists.
- Using statistical analysis of social media profiles to identify people likely to protest against the government.
- Using statistical analysis of social media profiles to identify people to target with political adverts.
- Using statistical analysis of social media profiles to target ads at people likely to buy a bicycle.
- Using statistical analysis of social media profiles to target ads at people likely to gamble at a new online casino. Does it matter to you if it’s an ad for the casino or for help for gambling addiction?
The use and misuse of statistical inference offer many ethical dilemmas. Some common issues related to ethics and good statistical practice are discussed below. As you read them and work with the associated exercises, consider consulting the ASA’s ethical guidelines, presented above.
3.11.2 p-hacking and the file-drawer problem
Hypothesis tests are easy to misuse. If you run enough tests on your data, you are almost guaranteed to end up with significant results – either due to chance or because some of the null hypotheses you test are false. The process of trying lots of different tests (different methods, different hypotheses, different subgroups) in search of significant results is known as p-hacking, p-fishing, or data dredging. This greatly increases the risk of false findings and can often produce misleading results.
Many practitioners inadvertently resort to p-hacking, by mixing exploratory data analysis and hypothesis testing, or by coming up with new hypotheses to test as they work with their data. This can be avoided by planning your analyses in advance, a practice that in fact is required in medical trials.
On the other end of the spectrum, there is the file-drawer problem, in which studies with negative (i.e., not statistically significant) results aren’t published or reported but instead are stored in the researcher’s file drawers. There are many reasons for this, one being that negative results usually are seen as less important and less worthy of spending time on. Simply put, negative results just aren’t news. If your study shows that eating kale every day significantly reduces the risk of cancer, then that is news, something that people are interested in learning, and something that can be published in a prestigious journal. However, if your study shows that a daily serving of kale has no impact on the risk of cancer, that’s not news, people aren’t really interested in hearing it, and it may prove difficult to publish your findings.
But what if 100 different researchers carried out the same study? If eating kale doesn’t affect the risk of cancer, then we can still expect five out of these researchers to get significant results (using a 5% significance level). If only those researchers publish their results, that may give the impressions that there is strong evidence of the cancer-preventing effect of kale backed up by several papers, even though the majority of studies actually indicated that there was no such effect.
\[\sim\]
Exercise 3.10 Discuss the following. You are helping a research team with statistical analysis of data that they have collected. You agree on five hypotheses to test. None of the tests turns out to be significant. Fearing that all their hard work won’t lead anywhere, your collaborators then ask you to carry out five new tests. Neither turns out to be significant. Your collaborators closely inspect the data and then ask you to carry out 10 more tests, two of which are significant. The team wants to publish these significant results in a scientific journal. Should you agree to publish them? If so, what results should be published? Should you have put your foot down and told them not to run more tests? Does your answer depend on how long it took the research team to collect the data? What if the team won’t get funding for new projects unless they publish a paper soon? What if other research teams competing for the same grants do their analyses like this?
Exercise 3.11 Discuss the following. You are working for a company that is launching a new product, a hair loss treatment. In a small study, the product worked for 19 out of 22 participants (86%). You compute a 95% Clopper-Pearson confidence interval (Section 3.5.1) for the proportion of successes and find that it is (0.65, 0.97). Based on this, the company wants to market the product as being 97% effective. Is that acceptable to you? If not, how should it be marketed? Would your answer change if the product was something else (new running shoes that make you faster, a plastic film that protects smartphone screens from scratches, or contraceptives)? What if the company wanted to market it as being 86% effective instead?
Exercise 3.12 Discuss the following. You have worked long and hard on a project. In the end, to see if the project was a success, you run a hypothesis test to check if two variables are correlated. You find that they are not (p = 0.15). However, if you remove three outliers, the two variables are significantly correlated (p = 0.03). What should you do? Does your answer change if you only have to remove one outlier to get a significant result? If you have to remove 10 outliers? 100 outliers? What if the p-value is 0.051 before removing the outliers and 0.049 after removing the outliers?
Exercise 3.13 Discuss the following. You are analysing data from an experiment to see if there is a difference between two treatments. You estimate23 that given the sample size and the expected difference in treatment effects, the power of the test that you’ll be using, i.e., the probability of rejecting the null hypothesis if it is false, is about 15%. Should you carry out such an analysis? If not, how high does the power need to be for the analysis to be meaningful?
3.11.3 Reproducibility
An analysis is reproducible if it can be reproduced by someone else. By producing reproducible analyses, we make it easier for others to scrutinise our work. We also make all the steps in the data analysis transparent. This can act as a safeguard against data fabrication and data dredging.
In order to make an analysis reproducible, we need to provide at least two things. First, the data – all unedited data files in their original format. This also includes metadata with information required to understand the data (e.g., codebooks explaining variable names and codes used for categorical variables). Second, the computer code used to prepare and analyse the data. This includes any wrangling and preliminary testing performed on the data.
As long as we save our data files and code, data wrangling and analyses in R are inherently reproducible, in contrast to the same tasks carried out in menu-based software such as Excel. However, if reports are created using a word processor, there is always a risk that something will be lost along the way. Perhaps numbers are copied by hand (which may introduce errors), or maybe the wrong version of a figure is pasted into the document. R Markdown (Section 4.1) is a great tool for creating completely reproducible reports, as it allows you to integrate R code for data wrangling, analyses, and graphics in your report-writing. This reduces the risk of manually inserting errors and allows you to share your work with others easily.
\[\sim\]
Exercise 3.14 Discuss the following. You are working on a study at a small-town hospital. The data involves biomarker measurements for a number of patients, and you show that patients with a sexually transmitted disease have elevated levels of some of the biomarkers. The data also includes information about the patients: their names, ages, zip codes, heights, and weights. The research team wants to publish your results and make the analysis reproducible. Is it ethically acceptable to share all your data? Can you make the analysis reproducible without violating patient confidentiality?
For instance, if the lady got 3 cups where the milk was poured first right, she must have got 1 cup wrong, so that the upper right cell should have the value 1. Then, because the column sums are 4, the lower left cell has the value 1 and the lower right cell has the value 3.↩︎
Either by using combinatorics and the classical definition of probability, or by using a hypergeometric distribution. Both approaches yield the same results.↩︎
The excerpt is from the version of the guidelines dated April 2018 and presented here with permission from the ASA.↩︎
We’ll discuss methods for producing such estimates in Section 7.2.3.↩︎